CGAL的三维曲面网格生成

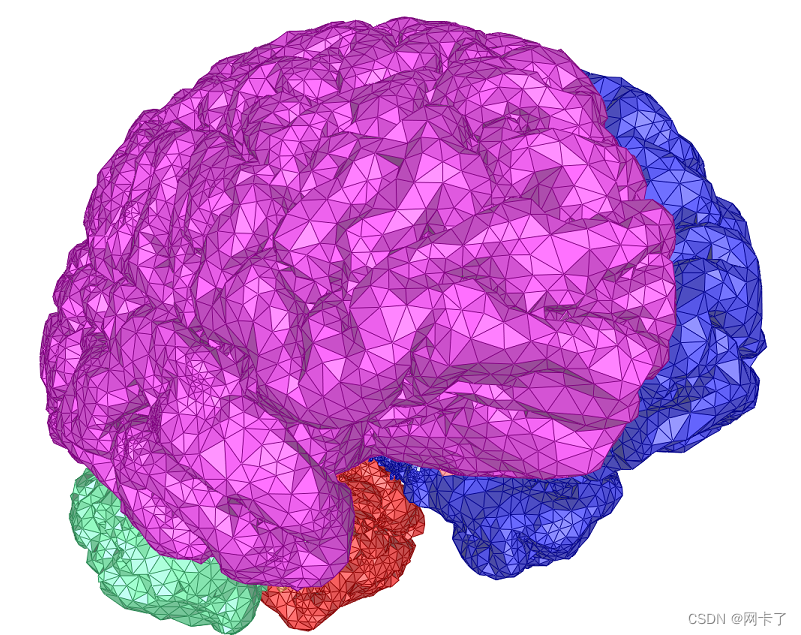
本文介绍: 此程序包提供了一个函数模板，用于计算三角网格，以近似表面。网格化算法要求仅通过一个能够判断给定线段、直线或射线是否与曲面相交，并且如果相交则计算交点的oracle来了解待网格化的表面。这一特性使该软件包具有足够的通用性，可以应用于各种情况。例如，它可以用于网格化隐式曲面，如某些函数的零水平集。它也可以用于医学成像领域，网格化三维图像中的灰度级集曲面。网格化算法基于受限的Del auna y 三角剖分概念。该算法基本上是在曲面上计算一组采样点，并从这些采样点的三维三角剖分中提取插值曲面网格。

1、介绍

此程序包提供了一个函数模板，用于计算三角网格，以近似表面。

网格化算法要求仅通过一个能够判断给定线段、直线或射线是否与曲面相交，并且如果相交则计算交点的oracle来了解待网格化的表面。这一特性使该软件包具有足够的通用性，可以应用于各种情况。例如，它可以用于网格化隐式曲面，如某些函数的零水平集。它也可以用于医学成像领域，网格化三维图像中的灰度级集曲面。

网格化算法基于受限的Del auna y 三角剖分概念。该算法基本上是在曲面上计算一组采样点，并从这些采样点的三维三角剖分中提取插值曲面网格。与Del auna y细化过程一样，迭代地将点添加到采样中，直到满足曲面网格元素的一些尺寸和形状标准。

尺寸和形状标准指导细化过程的行为并控制其终止。它们还决定了最终网格中元素的大小和形状。自然地，这些标准可以定制以满足用户需求。曲面网格生成包提供了一组可以通过三个数值进行缩放的标准。此外，用户还可以插入自己的一组细化标准。

如果用户能够在每个连接的组件上提供一个初始采样点，则对表面的拓扑和组件数量没有限制。如果表面足够光滑，并且尺寸标准足够小，则算法保证输出网格与表面同胚，并且与表面之间的距离很小（豪斯多夫距离甚至弗雷歇距离）。该算法也可用于非光滑表面，但无法保证。

2、用于光滑曲面的曲面网格生成器 接口

网格划分过程是通过调用函数模板来启动的。网格划分函数有两种重载版本，其特征如下：

template &lt;class SurfaceMeshC2T3,
          class Surface,
          class FacetsCriteria,
          class Tag &gt;
void make_surface_mesh(SurfaceMeshC2T3&amp; c2t3,
                       Surface surface,
                       FacetsCriteria criteria,
                       Tag);
template&lt; class SurfaceMeshC2T3,
          class SurfaceMeshTraits,
          class FacetsCriteria,
          class Tag &gt;
void make_surface_mesh(SurfaceMeshC2T3&amp; c2t3,
                       SurfaceMeshTraits::Surface_3 surface,
                       SurfaceMeshTraits traits,
                       FacetsCriteria criteria,
                       Tag );

模板参数 SurfaceMeshC2T3 表示用于存储表面网格的数据结构类型。此类型需要是概念 SurfaceMeshCo mplex _2InTriang ulation _3 的模型。此类数据结构具有指向三维三角剖分的指针，并将表面网格编码为此三角剖分中面的子集。类型 SurfaceMeshC2T3 的参数通过引用传递给网格化函数。此参数在过程结束时保存输出网格。

模板参数 Surface 表示表面类型。该类型必须是概念 Surface_3 的模型。

表面网格生成器所需的表面知识被封装在一个 trai ts 类中。实际上，网格生成器仅通过此 traits 类访问要网格化的表面。traits 类需要是概念 SurfaceMesh_Traits_3 的模型。 make_surface_mesh() 的两个重载版本之间的区别可以解释如下

在 make_surface_mesh() 的第一个重载版本中，表面类型作为模板参数给出，要网格化的表面作为参数传递给网格生成器。在这种情况下，表面网格生成器特征类型由一个名为 Surface_mesh_traits_generator_3 的辅助类从表面类型自动生成。

在 make_surface_mesh() 的第二个重载版本中，表面网格生成器特征类型由模板参数 SurfaceMeshTraits_3 提供，表面类型从此特征类型获得。表面和特征都作为参数传递给网格生成器。

当表面类型提供嵌套类型 Surface::Surface_mesher_traits_3 作为 SurfaceMesh Traits_3 的模型，或者提供 traits 生成器 Surface_mesh_traits_generator_3<Surface> 的特化的表面类型时，可以使用第一个重载版本。目前，该库为隐式表面（Im pli cit_surface_3<Traits, Funct ion>）和灰度图像（Gray_level_image_3<FT, Po int>）提供了 Surface_mesh_traits_generator_3<Surface> 的部分特化。

参数标准处理驱动网格划分过程的大小和形状标准的描述。模板参数FacetsCriteria必须由概念SurfaceMeshFacetsCriteria_3的模型实例化。

参数Tag是一个标签，其类型会影响网格算法的行为。例如，此参数可用于强制输出网格的流形属性，同时避免网格的过度细化。

调用 make_surface_mesh(c2t3,surface, criteria, tag) 会启动网格化过程，并使用一组初始点，该组初始点是两个子集的并集：c2t3 指向的初始三角剖分中的顶点集，以及 traits 类的 Con struct_initial_points() 函子提供的一组点。该初始点集需要包含要网格化的曲面的每个连通分量上的至少一个点。

3、输入输出

使用函数 CGAL::output_surface_facets_to_off()可以将表面网格输出为OFF格式。

4、网格生成标准、保证、变化

输出网格的保证取决于网格标准。首先，如果面角度的下限不大于30度，则证明网格算法终止。此外，输出网格保证与表面同胚，并且如果半径范围处处小于（epsi lon)倍局部特征尺寸，则网格和表面之间的距离（豪斯多夫距离甚至弗雷歇距离）有保证的范围。这里（epsilon)是一个必须小于0.16的常数，局部特征尺寸（mathrm{lfs}(x)）在表面的每个点（x）上定义为从（x）到中轴的距离。请注意，半径范围不需要是均匀的，尽管在默认标准中是均匀的。

当然，这样的理论保证只能针对具有有限非零到达值的平滑表面来实现。（表面的到达值是该表面上局部特征尺寸的最小值）。

曲面任何点上的局部特征尺寸值或曲面上的最小值通常是未知的，尽管有时可以猜测。此外，经常发生的情况是，设置网格标准以满足理论条件会产生过度细化的网格。另一方面，当尺寸标准放宽时，不能保证与输入曲面具有同胚性，并且不能保证输出网格是流形。为了解决这个问题，并给出更灵活的网格算法，函数模板 make_surface_mesh() 有一个标记模板参数，可以稍微改变细化过程的行为。这个功能允许，例如，使用放宽的尺寸标准运行网格算法，与用户期望的网格尺寸更加一致，并且仍然保证输出网格形成流形表面。函数 make_surface_mesh() 具有以下标记类型的专用版本：Manifold_tag：输出网格保证为无边界的流形曲面。Manifold_wi th_boundary_tag：输出网格保证是流形，但可能有边界。Non_manifold_tag：该算法依赖于给定的标准，并且不保证其他任何东西。

5、输出

该CGAL组件还提供将重建的曲面网格写入对象文件格式（OFF）[2]并将其转换为FaceGraph（当它是流形时）的功能：output_surface_facets_to_off()；out put_surface_facets_to_polyhedron()；facets_in_com plex_2_to_triangle_mesh()。