本文介绍: 并且对于任意时间步 nn,都有 P(Xn+1=j)=∑iP(Xn=i)⋅P(Xn+1=j∣Xn=i)P(Xn+1=j)=∑iP(Xn=i)⋅P(Xn+1=j∣Xn=i),其中 P(Xn=i)P(Xn=i) 表示在时间步 nn 处于状态 ii 的概率,那么向量 ππ 就是该马尔可夫链的稳态分布。马尔可夫链(Markov Chain)是一种随机过程,具有“马尔可夫性质”,即在给定当前状态的条件下,未来状态的概率分布仅依赖于当前状态,而与过去状态无关。稳态分布的存在性和唯一性取决于具体的马尔可夫链。
马尔可夫链(Markov Chain)是一种随机过程,具有“马尔可夫性质”,即在给定当前状态的条件下,未来状态的概率分布仅依赖于当前状态,而与过去状态无关。马尔可夫链在很多领域都有广泛的应用,包括蒙特卡洛方法、统计物理学、自然语言处理等。
马尔可夫链的一般定义如下:
给定状态空间 SS 和状态转移概率矩阵 PP,其中 PijPij 表示从状态 ii 转移到状态 jj 的概率,如果对于任意状态 i,ji,j 和任意时间步 nn,满足以下条件,则称该过程是马尔可夫链:
P(Xn+1=j∣X0,X1,…,Xn)=P(Xn+1=j∣Xn)
P(Xn+1=j∣X0,X1,…,Xn)=P(Xn+1=j∣Xn)
其中,XnXn 表示在时间步 nn 的状态。
马尔可夫链的一个重要特性是它在长时间内具有收敛性,即在足够长的时间后,马尔可夫链的状态分布会收敛到一个稳态分布。这个性质是许多马尔可夫链算法应用的基础。
马尔可夫链的稳态分布表示在长时间运行后,随机过程中各个状态的概率分布不再随时间变化,保持恒定的概率分布。
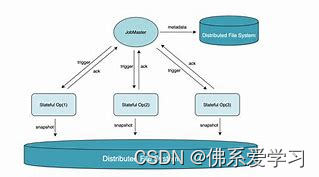
这个是实例:
稳态分布(Stationary Distribution)是指在马尔可夫链达到平稳状态后,随机过程中各个状态的概率分布不再随时间变化,保持恒定的概率分布。换句话说,稳态分布是一个时间不变的分布,表示在长时间运行后,随机过程在不同状态的停留概率。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。