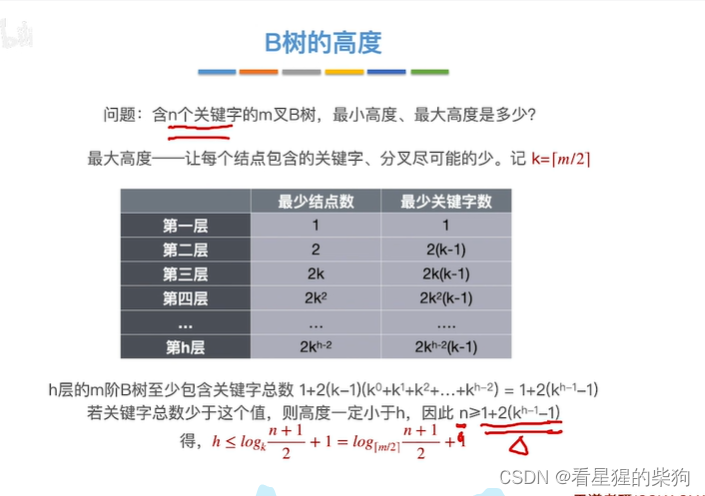
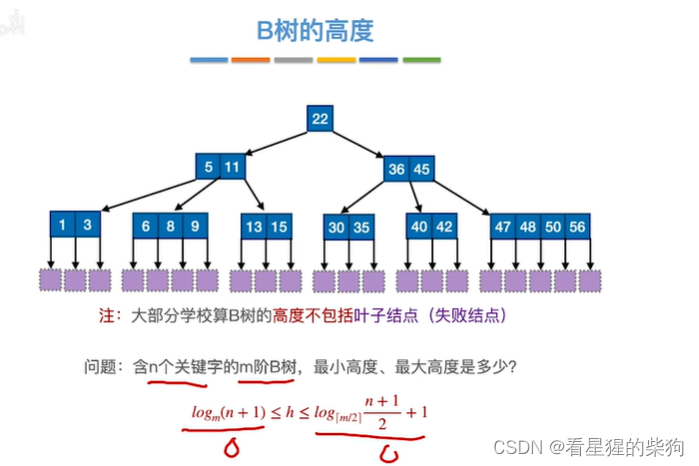
本文介绍: 所以高度为h的最高的B树，此时的叶子节点树最小就是图中等比得来的，最大得小于终端节点的关键字总数可以多到为此时等比得来得叶子节点的关键字的数模加上终端节点关键字数目，若等于，此时高度还可以增加了。此时假设此时h为最高的B树的高度，那么此时高度最高的B树的除终端节点的节点的关键字数目必须为最小节点关键字总数，终端节点的关键字数目可以大于等于节点最小关键字总数。所以此时关键字数目为n的对应的最高的高度为h的B树的叶子节点的关键字的数目一定是大于最高的高度为h的B树的叶子节点的最少数目（等比得来的）
回顾：二叉查找树
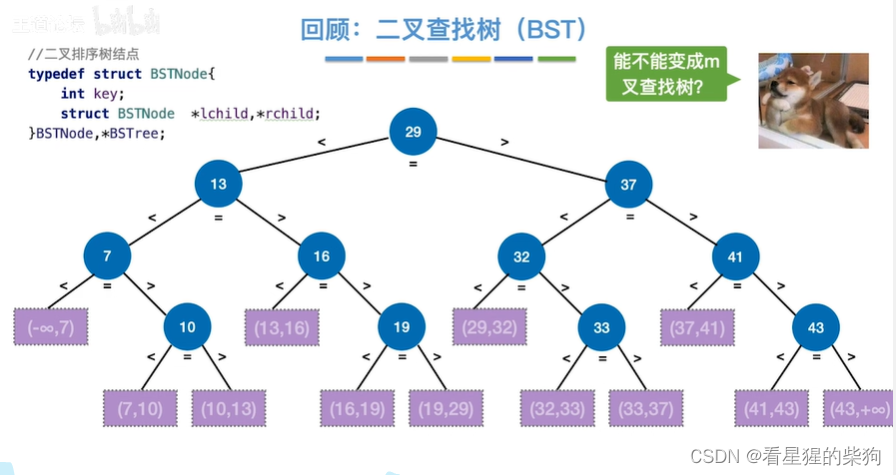
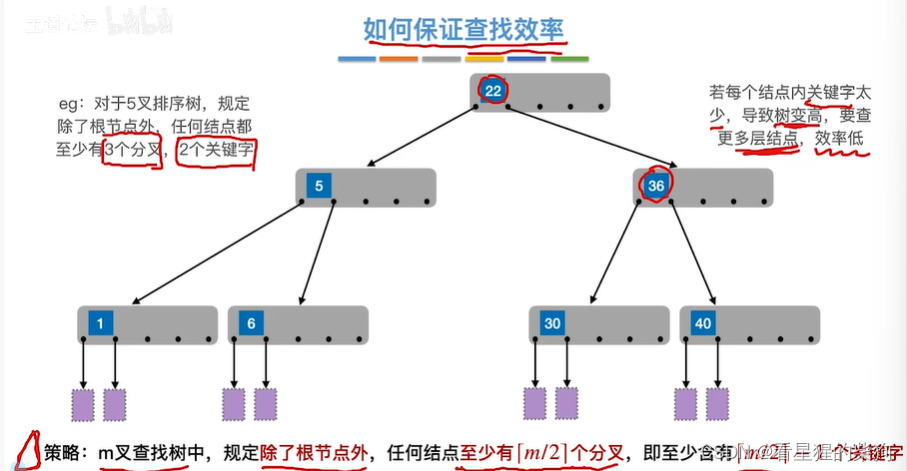
五叉查找树
进一步对范围划分，处于不同划分进入不同子树
四个数做划分，此时有五个区间
此时一个节点对应多个关键字,如果叶子节点依然没有对应的关键字，那么即查找失败，然后看看在叶子节点的关键字的哪个区间
此时每个节点可以只有一个关键字，也可以有多个关键字，其对应的子树个数自然也就不同
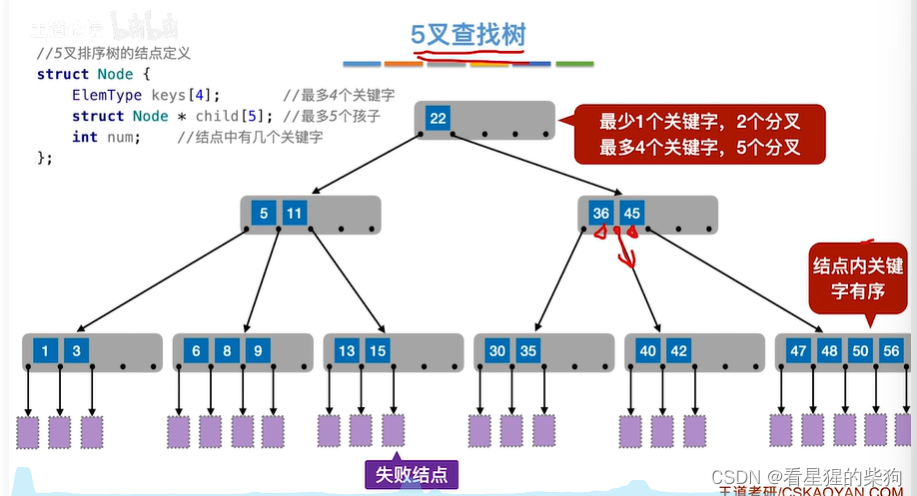
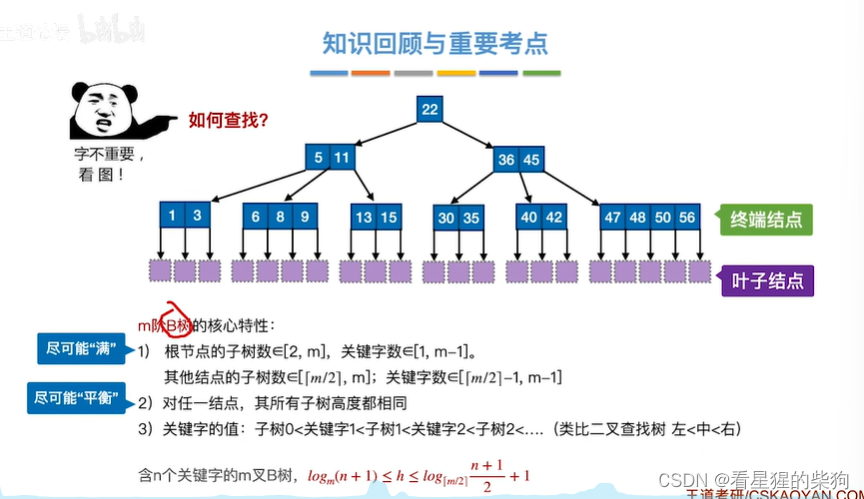
如何查找
查找成功
9小于22，进入左子树，到左子树的根节点，此时比对关键字，可以顺序找，也可以折半找，此时没找到，但范围区间找到了，此时跳到三个子树的第二个子树上，再次顺序查找，发现找到对应的关键字，查找成功
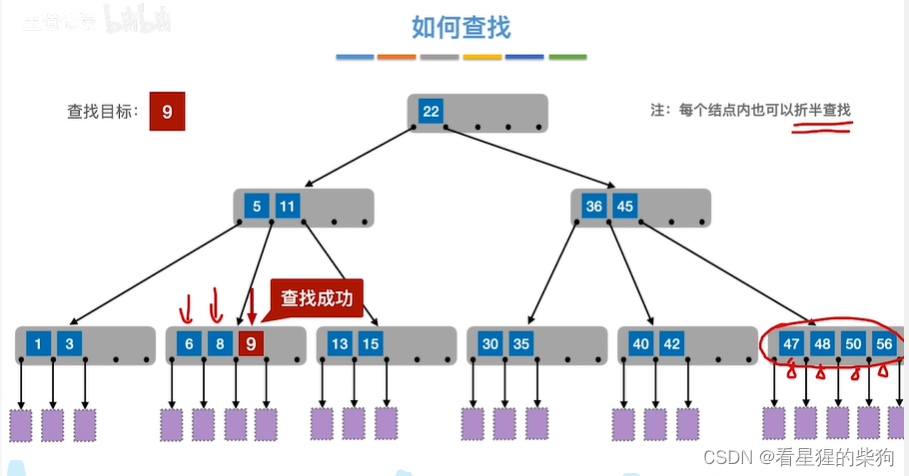
查找失败
41大于22，首先到右子树去，比对关键字，在对应的第二个子树，进入该子树，再次比对关键字，此时进入对应的第二子树，但此时为空，所以没找到
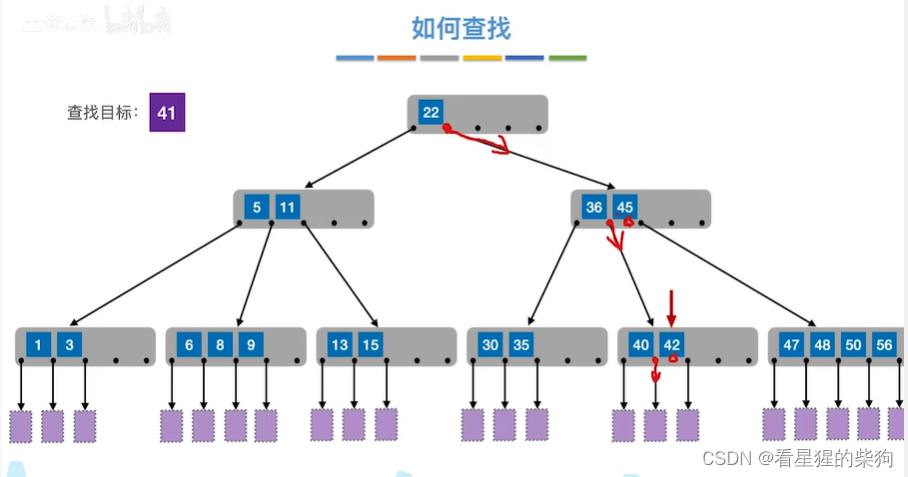
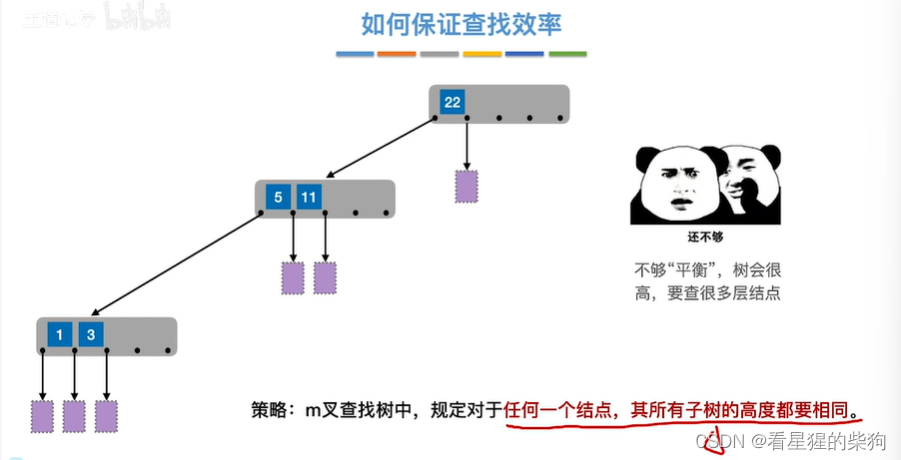
如何保证查找效率
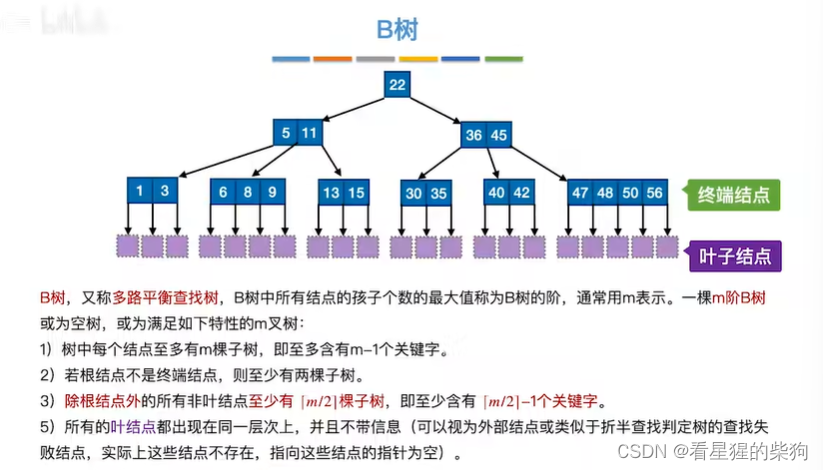
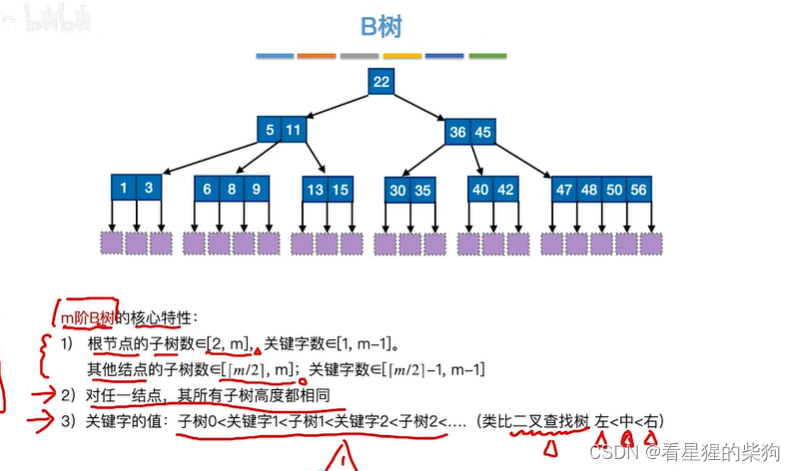
B树
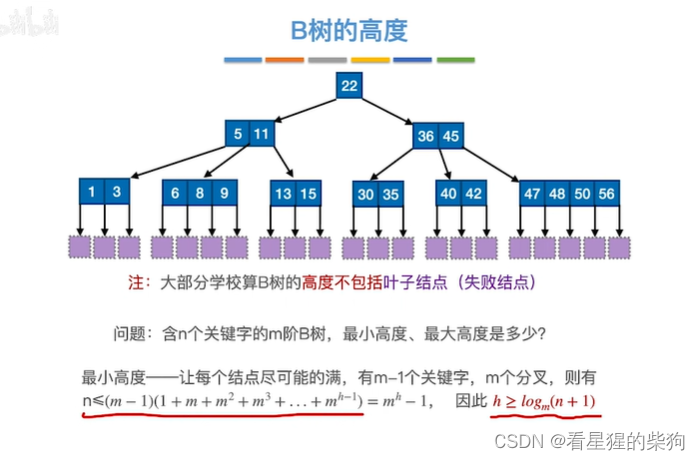
B树的高度
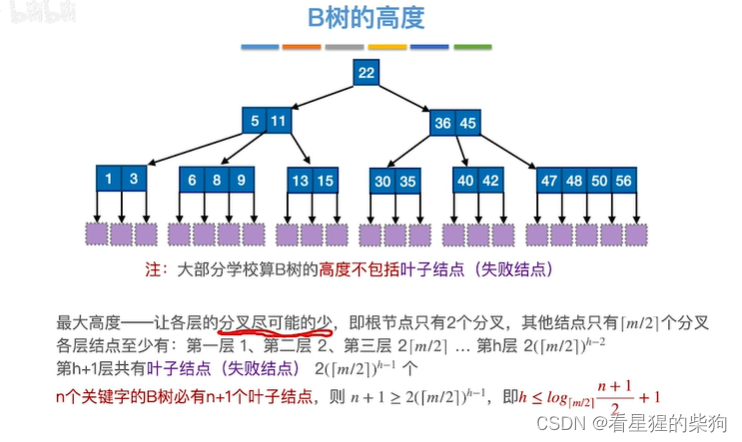此时利用的是如果关键字总数小于当每个节点的关键字都是最少时构成的树的关键字总数的话，那么此时高度一定小于h，因为此时若依然为h，那么此时由于任何一个节点都不能有更少的关键字，所以失败。所以如果此时最大高度为h时，那么此时关键字总数一定大于高度为h当每个节点的关键字都是最少时构成的树的关键字总数
小结
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
