本文介绍: 机器学习_捕捉函数的变化趋势(凸函数)
机器学习所关心的问题之一捕捉函数的变化趋势,也就是标签(y)是如何随着特征字段(x)而变化的,这个变化趋势是通过求导和微分来实现的。
连续性是求导的前提条件
具有连续性的函数,y值随x值的变化是连贯不间断的。
并不是所有函数都具有连续性,像上面提到的阶跃函数从-1到1的跃迁明显就不具有连续性。
通过求导发现 y 如何随 x 而变
导数是定义在连续函数的基础之上的。想要对函数求导,函数至少要有一段是连续的。
当A点和B点的距离越来越小,两个点无限接近,逼近极限的时候,在即将重合而又未重合的一刹那,割线就变成切线了,如下图所示:
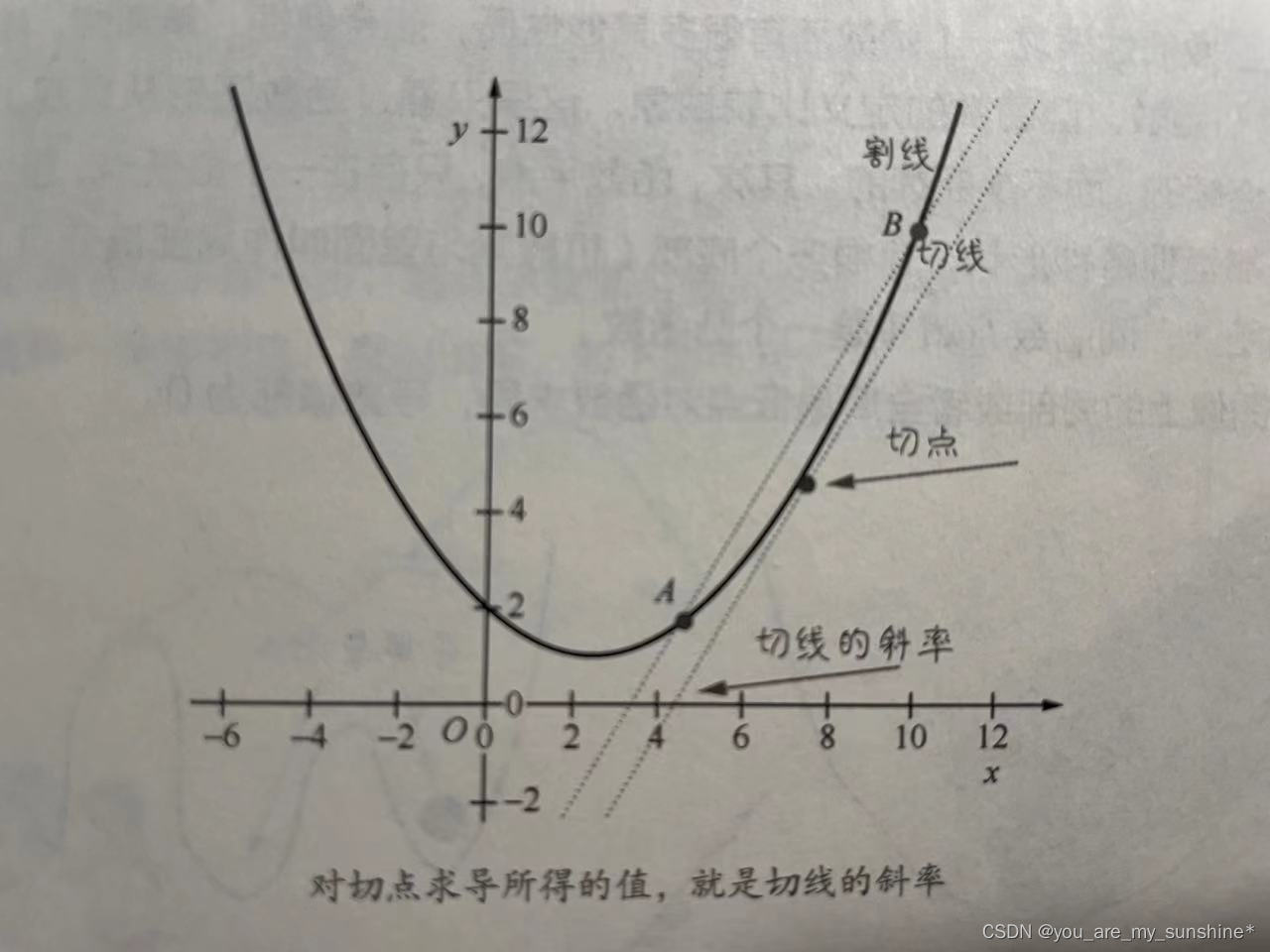
而此时,对切点求导所得的值,就是切线的斜率。
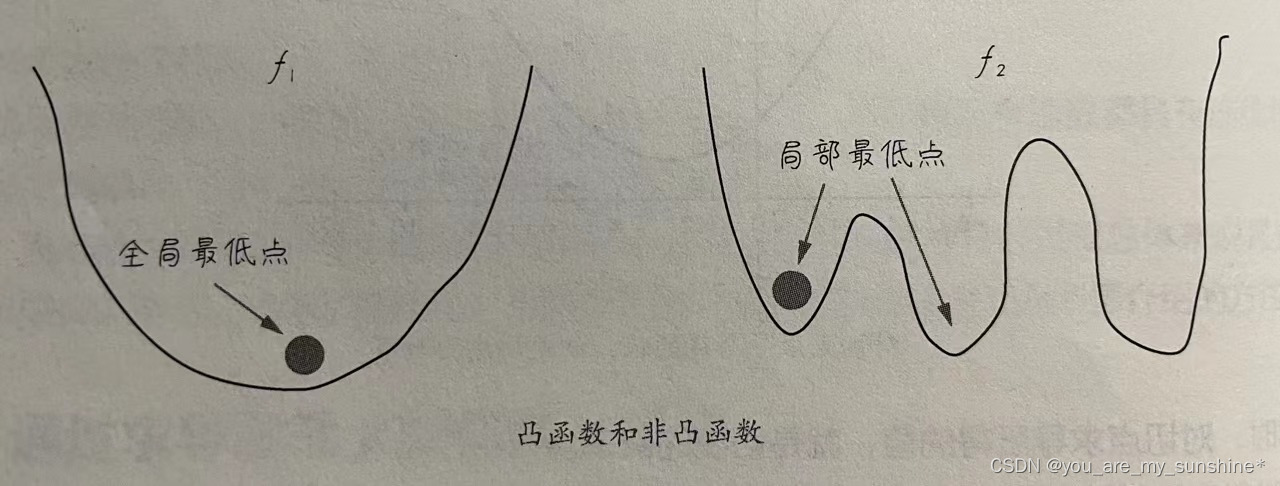
凸函数有一个全局最低点
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。