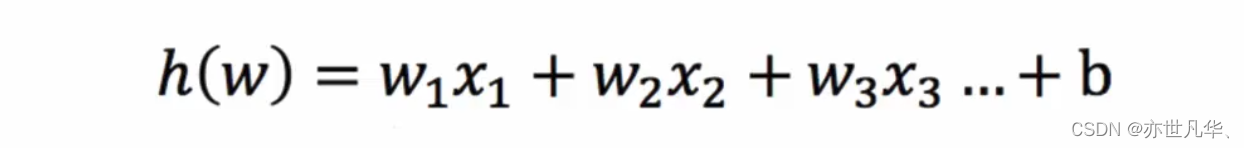本文介绍: 比如举个例子,有3个数1,2,3 ,那么用1 / (1+2+3) 2/ (1+2+3) 3/ (1+2+3) 这样得到的概率,加起来就是1对吧,一个道理。- 对于类别{1, 2},比较1和2之间的年龄差异,可以得到1比2年轻,因此1属于一类,2属于另一类。- 对于类别{1, 3},比较1和3之间的年龄差异,可以得到1比3年轻,因此1属于一类,3属于另一类。1. 首先,将三个人分别标记为1、2和3,形成三个类别:{1, 2}, {1, 3}和{2, 3}。
然后我们再来看一下如何我们自己使用代码实现逻辑回归的,对二分类以上,比如三分类的概率计算

首先我们把公式写出来
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。