文章目录
- 一、有向图模型
-
- 1. 贝叶斯网络的定义
- 2. 条件独立性及其证明
-
- a. 间接因果关系
X
3
→
X
2
→
X
1
X_3 rightarrow X_2 rightarrow X_1
X3→X2→X1
- b. 间接果因关系
X
1
→
X
2
→
X
3
X_1 rightarrow X_2 rightarrow X_3
X1→X2→X3
- c. 共因关系
X
1
←
X
2
→
X
3
X_1 leftarrow X_2 rightarrow X_3
X1←X2→X3
- d. 共果关系
X
1
→
X
2
←
X
3
X_1 rightarrow X_2 leftarrow X_3
X1→X2←X3
- a. 间接因果关系
- 3. 局部马尔可夫性质
- 二、常见的有向图模型
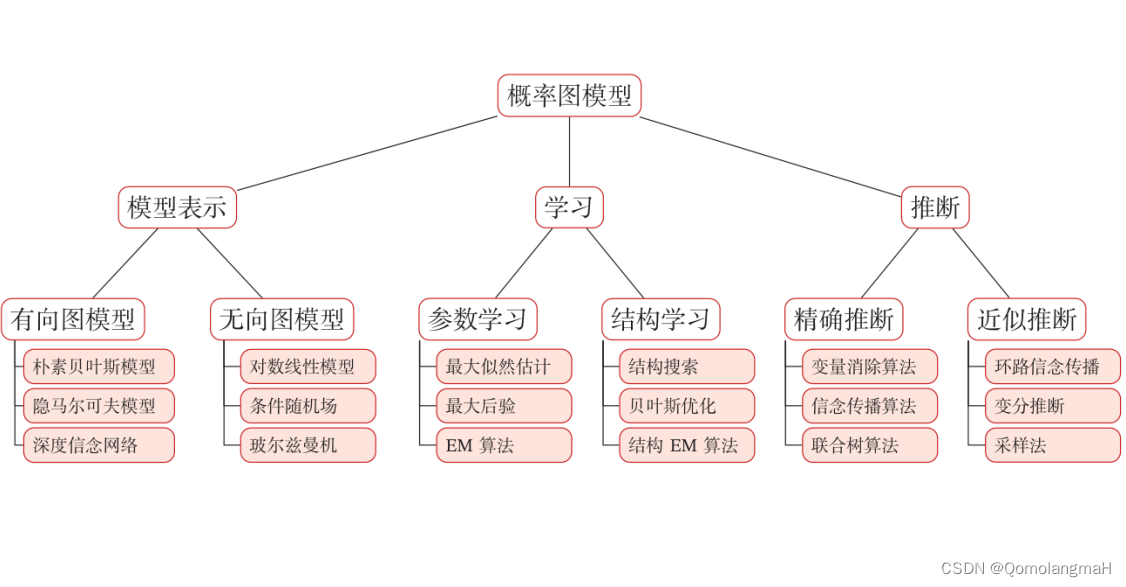
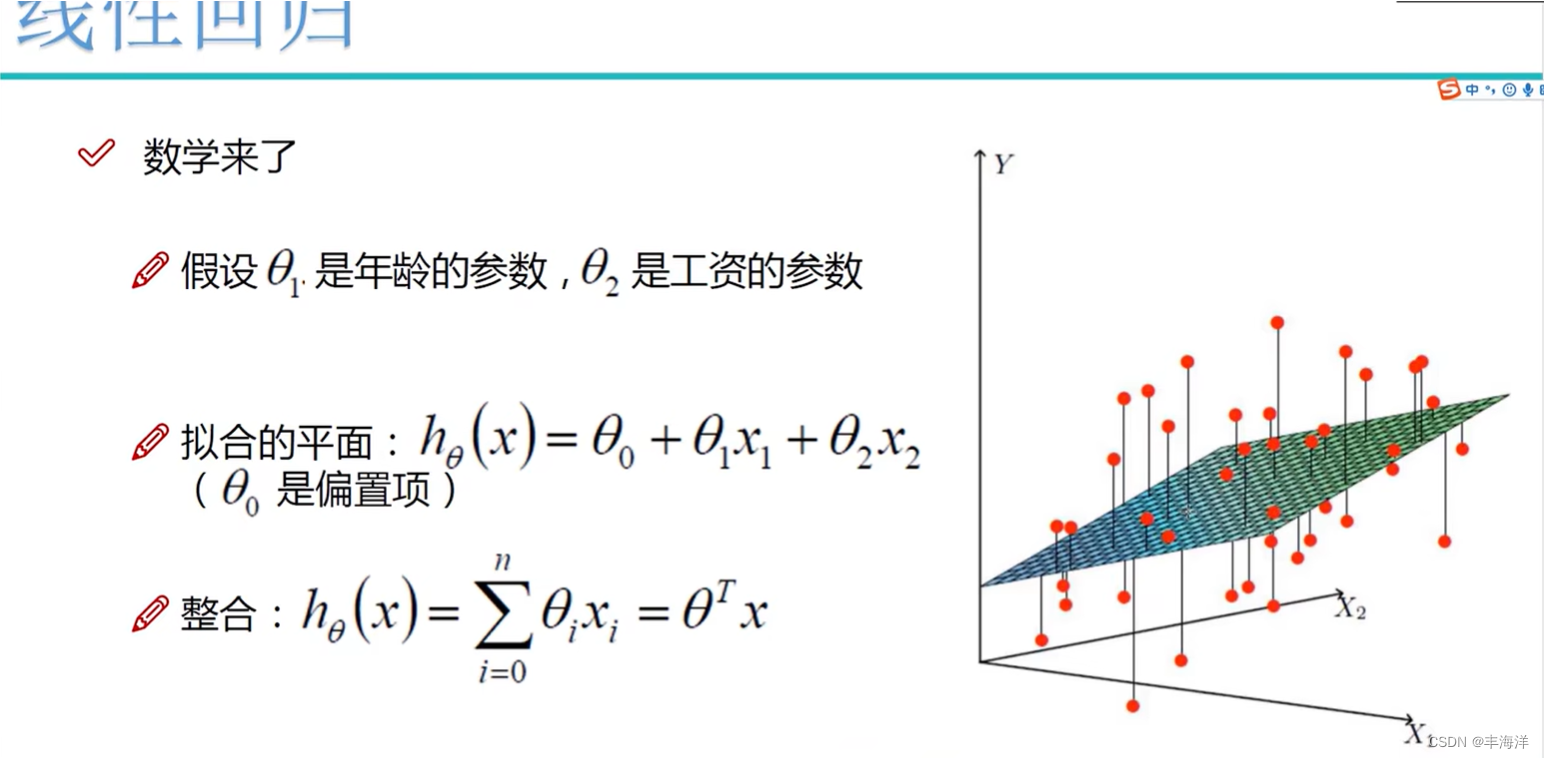
概率图模型(Probabilistic Graphical Model,PGM)是一种用图结构来表示和推断多元随机变量之间条件独立性的概率模型。图模型提供了一种直观且有效的方式来描述高维空间中的概率分布,通过图结构表示随机变量之间的关系,使得模型的参数量得以减少。
一、有向图模型
有向图模型(Directed Graphical Models)是概率图模型的一类,其中最为知名的代表是贝叶斯网络。这种模型在处理多变量概率关系方面表现出色,提供了一种直观、清晰的方法来描述随机变量之间的因果关系。
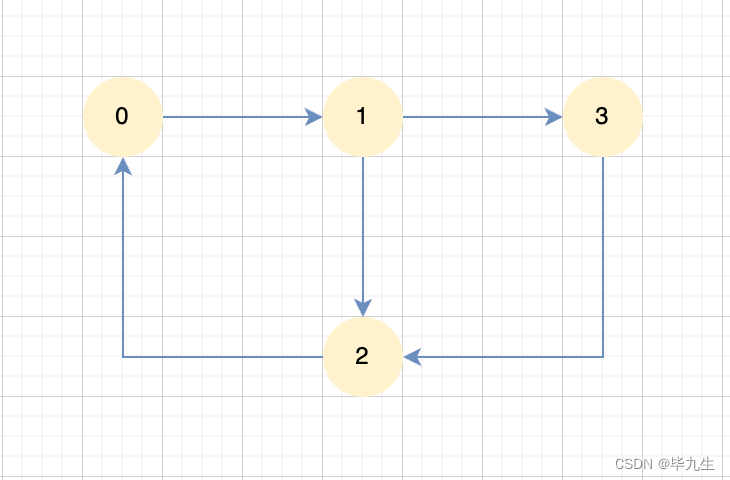
1. 贝叶斯网络的定义

-
有向非循环图
G
G
G:
G
G
G是一个图,其中每个边都有一个方向,而且没有形成循环,每个节点都表示一个随机变量。这种有向图表示了变量之间的因果关系,其中箭头的方向指示了因果关系的方向。
-
X
X
X 是一个
K
K
K
K
X
X
-
X
π
X
k
X_k
Xk 的所有父节点变量的集合,这是一个关键概念,它表示了图中节点
X
k
X_k
-
P
(
X
k
∣
X
π
k
)
P(X_k | X_{pi_k})
P(Xk∣Xπk):表示每个随机变量的局部条件概率分布,即给定其父节点的条件下,该变量的概率分布,表达了节点之间的因果关系。
-
X
X
X
k
X_k
(
)
=
∏
k
=
1
K
(
k
∣
π
k
)
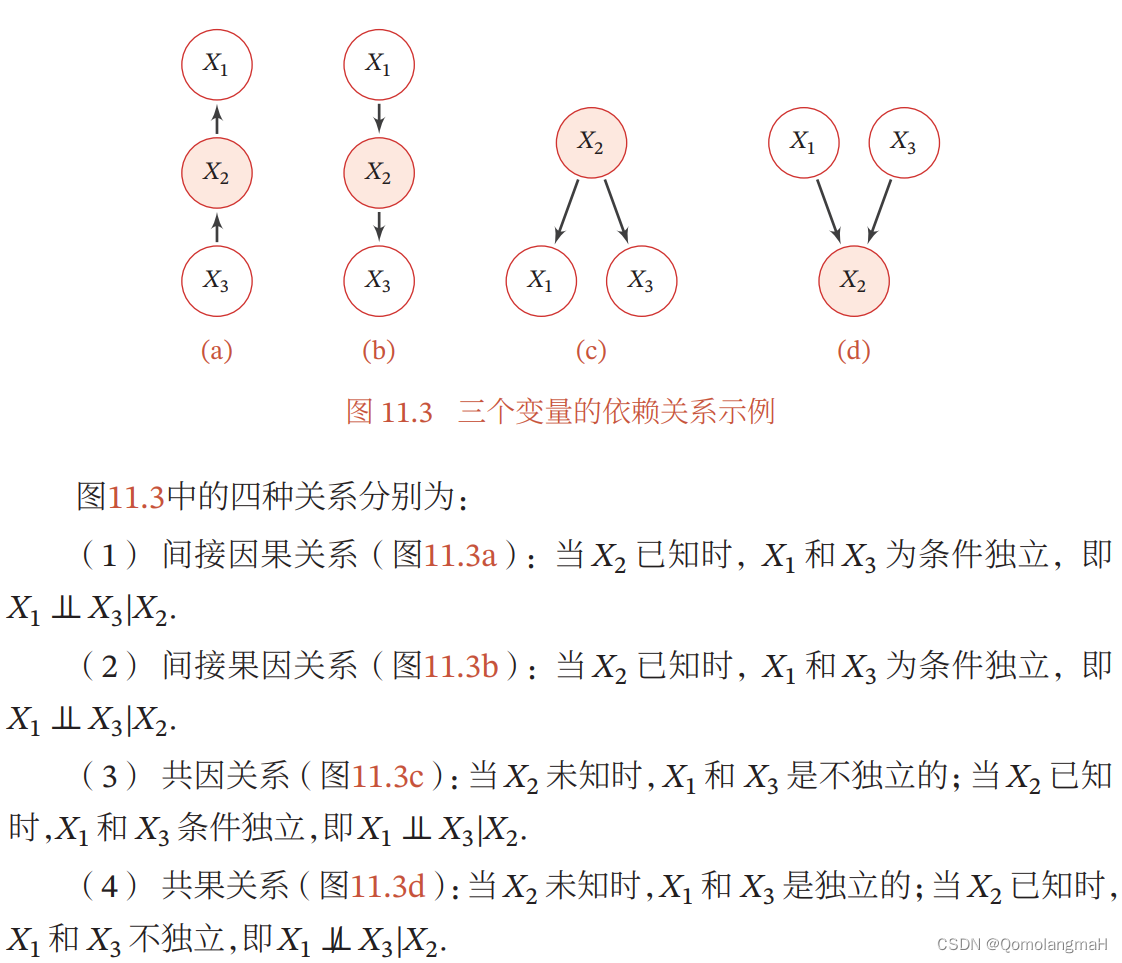
2. 条件独立性及其证明
⊥
perp
⊥符号说明:markdown没找到与教材相同符号,这里暂使用
⊥
perp
⊥替代
-
间接因果关系
X
3
→
X
2
→
X
1
X_3 rightarrow X_2 rightarrow X_1
X3→X2→X1:
-
间接果因关系
X
1
→
X
2
→
X
3
X_1 rightarrow X_2 rightarrow X_3
X1→X2→X3:
-
共因关系
X
1
←
X
2
→
X
3
X_1 leftarrow X_2 rightarrow X_3
X1←X2→X3:
-
共果关系
X
1
→
X
2
←
X
3
X_1 rightarrow X_2 leftarrow X_3
X1→X2←X3:
a. 间接因果关系
X
3
→
X
2
→
X
1
X_3 rightarrow X_2 rightarrow X_1
X3→X2→X1
在间接因果关系中,考虑
X
1
X_1
X1 和
X
3
X_3
X3 在给定
X
2
X_2
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
1
,
X
2
,
X
3
)
P
(
X
2
)
P(X_1, X_3 | X_2) = frac{P(X_1, X_2, X_3)}{P(X_2)}
P(X1,X3∣X2)=P(X2)P(X1,X2,X3)
P
(
X
1
,
X
2
,
X
3
)
=
P
(
X
3
)
⋅
P
(
X
2
∣
X
3
)
⋅
P
(
X
1
∣
X
2
)
P(X_1, X_2, X_3) = P(X_3) cdot P(X_2 | X_3) cdot P(X_1 | X_2)
P(X1,X2,X3)=P(X3)⋅P(X2∣X3)⋅P(X1∣X2)
将其代入条件概率的计算式中:
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
3
)
⋅
P
(
X
2
∣
X
3
)
P
(
X
2
)
⋅
P
(
X
1
∣
X
2
)
P(X_1, X_3 | X_2) = frac{P(X_3) cdot P(X_2 | X_3) }{P(X_2)}cdot P(X_1 | X_2)
P(X1,X3∣X2)=P(X2)P(X3)⋅P(X2∣X3)⋅P(X1∣X2)
因为(条件概率~贝叶斯公式)
P
(
X
2
,
X
3
)
=
P
(
X
3
)
⋅
P
(
X
2
∣
X
3
)
=
P
(
X
2
)
⋅
P
(
X
3
∣
X
2
)
P(X_2,X_3)=P(X_3) cdot P(X_2 | X_3) =P(X_2) cdot P(X_3 | X_2)
P(X2,X3)=P(X3)⋅P(X2∣X3)=P(X2)⋅P(X3∣X2)
所以
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
3
∣
X
2
)
⋅
P
(
X
1
∣
X
2
)
P(X_1, X_3 | X_2) = P(X_3 | X_2) cdot P(X_1 | X_2)
P(X1,X3∣X2)=P(X3∣X2)⋅P(X1∣X2)
得证,在
X
3
→
X
2
→
X
1
X_3 rightarrow X_2 rightarrow X_1
X3→X2→X1的关系下,
X
1
X_1
X1 和
X
3
X_3
X3 在给定
X
2
X_2
X2的条件下是独立的。
b. 间接果因关系
X
1
→
X
2
→
X
3
X_1 rightarrow X_2 rightarrow X_3
X1→X2→X3
- 概率链规则:
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
1
,
X
2
,
X
3
)
P
(
X
2
)
P(X_1, X_3 | X_2) = frac{P(X_1, X_2, X_3)}{P(X_2)}
P(X1,X3∣X2)=P(X2)P(X1,X2,X3)
- 联合概率的分解:
P
(
X
1
,
X
2
,
X
3
)
=
P
(
X
1
)
⋅
P
(
X
2
∣
X
1
)
⋅
P
(
X
3
∣
X
2
)
P(X_1, X_2, X_3) = P(X_1) cdot P(X_2 | X_1) cdot P(X_3 | X_2)
P(X1,X2,X3)=P(X1)⋅P(X2∣X1)⋅P(X3∣X2)
- 代入条件概率的计算式,得到:
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
1
)
⋅
P
(
X
2
∣
X
1
)
P
(
X
2
)
⋅
P
(
X
3
∣
X
2
)
P(X_1, X_3 | X_2) = frac{P(X_1) cdot P(X_2 | X_1) }{P(X_2)}cdot P(X_3 | X_2)
P(X1,X3∣X2)=P(X2)P(X1)⋅P(X2∣X1)⋅P(X3∣X2)
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
1
∣
X
2
)
⋅
P
(
X
3
∣
X
2
)
P(X_1, X_3 | X_2) = P(X_1 | X_2) cdot P(X_3 | X_2)
P(X1,X3∣X2)=P(X1∣X2)⋅P(X3∣X2)
- 得证,在
X
1
→
X
2
→
X
3
X_1 rightarrow X_2 rightarrow X_3
X1→X2→X3 的关系下,
X
1
X_1
X1 和
X
3
X_3
X3 在给定
X
2
X_2
X2 的条件下是独立的。
c. 共因关系
X
1
←
X
2
→
X
3
X_1 leftarrow X_2 rightarrow X_3
X1←X2→X3
- 联合概率的分解:
P
(
X
1
,
X
2
,
X
3
)
=
P
(
X
2
)
⋅
P
(
X
1
∣
X
2
)
⋅
P
(
X
3
∣
X
2
)
P(X_1, X_2, X_3) = P(X_2) cdot P(X_1 | X_2)cdot P(X_3 | X_2)
P(X1,X2,X3)=P(X2)⋅P(X1∣X2)⋅P(X3∣X2)
- 将其代入条件概率的计算式中:
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
1
∣
X
2
)
⋅
P
(
X
2
)
⋅
P
(
X
3
∣
X
2
)
P
(
X
2
)
P(X_1, X_3 | X_2) = frac{P(X_1 | X_2) cdot P(X_2) cdot P(X_3 | X_2)}{P(X_2)}
P(X1,X3∣X2)=P(X2)P(X1∣X2)⋅P(X2)⋅P(X3∣X2)
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
1
∣
X
2
)
⋅
P
(
X
3
∣
X
2
)
P(X_1, X_3 | X_2) = P(X_1 | X_2) cdot P(X_3 | X_2)
P(X1,X3∣X2)=P(X1∣X2)⋅P(X3∣X2)
- 这表明在
X
1
←
X
2
→
X
3
X_1 leftarrow X_2 rightarrow X_3
X1←X2→X3 的关系下,
X
1
X_1
X1 和
X
3
X_3
X3 在给定
X
2
X_2
X2 的条件下是独立的。
d. 共果关系
X
1
→
X
2
←
X
3
X_1 rightarrow X_2 leftarrow X_3
X1→X2←X3
- 联合概率的分解:
P
(
X
1
,
X
2
,
X
3
)
=
P
(
X
1
)
⋅
P
(
X
3
)
⋅
P
(
X
2
∣
X
1
,
X
3
)
P(X_1, X_2, X_3) = P(X_1) cdot P(X_3) cdot P(X_2 | X_1, X_3)
P(X1,X2,X3)=P(X1)⋅P(X3)⋅P(X2∣X1,X3)
- 将其代入条件概率的计算式中:
P
(
X
1
,
X
3
∣
X
2
)
=
P
(
X
1
)
⋅
P
(
X
3
)
⋅
P
(
X
2
∣
X
1
,
X
3
)
P
(
X
2
)
P(X_1, X_3 | X_2) = frac{P(X_1) cdot P(X_3) cdot P(X_2 | X_1, X_3)} {P(X_2)}
P(X1,X3∣X2)=P(X2)P(X1)⋅P(X3)⋅P(X2∣X1,X3)
- 这里的联合概率不能简化为
P
(
X
1
∣
X
2
)
⋅
P
(
X
3
∣
X
2
)
P(X_1 | X_2) cdot P(X_3 | X_2)
P(X1∣X2)⋅P(X3∣X2),这表明在
X
1
→
X
2
←
X
3
X_1 rightarrow X_2 leftarrow X_3
X1→X2←X3 的关系下,
X
1
X_1
X1 和
X
3
X_3
X3 在给定
X
2
X_2
X2的条件下不是独立的。
3. 局部马尔可夫性质
a. 理论
X
k
X_k
Xk,它在给定其父节点
X
π
k
X_{pi_k}
Xπk 的条件下,条件独立于与
X
k
X_k
Xk 不相关的其他节点
Z
Z
Z,即
P
(
X
k
∣
X
π
k
,
Z
)
=
P
(
X
k
∣
X
π
k
)
.
P(X_k | X_{pi_k}, Z) = P(X_k | X_{pi_k}).
P(Xk∣Xπk,Z)=P(Xk∣Xπk).
这表示,给定节点
X
k
X_k
Xk 的父节点的信息,节点
X
k
X_k
Xk 与其非后代节点
Z
Z
Z 之间没有直接的概率依赖关系,这个性质使得贝叶斯网络中的条件独立性关系更加清晰和易于推断。
b. 证明
P
(
X
k
,
Z
∣
X
π
k
)
=
P
(
X
k
,
Z
,
X
π
k
)
P
(
X
π
k
)
P(X_k, Z | X_{pi_k}) = frac{P(X_k, Z , X_{pi_k})}{P( X_{pi_k})}
P(Xk,Z∣Xπk)=P(Xπk)P(Xk,Z,Xπk)
P
(
X
k
,
Z
∣
X
π
k
)
=
P
(
X
π
k
)
⋅
P
(
X
k
∣
X
π
k
)
⋅
P
(
Z
∣
X
π
k
,
X
k
)
P
(
X
π
k
)
P(X_k, Z | X_{pi_k}) = frac{P(X_{pi_k})cdot P(X_k|X_{pi_k}) cdot P(Z|X_{pi_k},X_k) }{P( X_{pi_k})}
P(Xk,Z∣Xπk)=P(Xπk)P(Xπk)⋅P(Xk∣Xπk)⋅P(Z∣Xπk,Xk)
P
(
X
k
,
Z
∣
X
π
k
)
=
P
(
X
k
∣
X
π
k
)
⋅
P
(
Z
∣
X
π
k
,
X
k
)
P(X_k, Z | X_{pi_k}) = P(X_k|X_{pi_k}) cdot P(Z|X_{pi_k},X_k)
P(Xk,Z∣Xπk)=P(Xk∣Xπk)⋅P(Z∣Xπk,Xk)
P
(
X
k
,
Z
∣
X
π
k
)
=
P
(
X
k
∣
X
π
k
)
⋅
P
(
Z
∣
X
π
k
)
P(X_k, Z | X_{pi_k}) = P(X_k|X_{pi_k}) cdot P(Z|X_{pi_k})
P(Xk,Z∣Xπk)=P(Xk∣Xπk)⋅P(Z∣Xπk)
二、常见的有向图模型
1. Sigmoid信念网
2. 朴素贝叶斯分类器
3. 隐马尔可夫模型
原文地址:https://blog.csdn.net/m0_63834988/article/details/134633334
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_39678.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!



![[技术杂谈]如何下载vscode历史版本](https://img-blog.csdnimg.cn/direct/18e927e78e82496e80649940eb70a716.png)