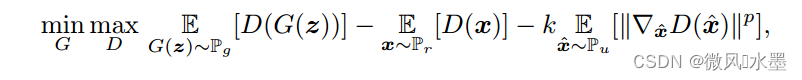本文介绍: 在计算机视觉的许多领域中,生成对抗性网络已经取得了巨大的成功,其中WGANs系列被认为是最先进的,主要是由于其理论贡献和竞争的定性表现。在 WGAN-gp 中,为了满足 1-Lipschitz 约束,训练出好效果,采用了真假数据的插值方法,来模拟全空间的均匀分布。WGAN-div 的作者说,这种做法是一种机械性的,很难靠有限的采样,模拟出这种全空间分布。作者提出了一种新的 Wasserstein 散度(W-div),它是W-met的松弛版本,不需要k-Lipschitz约束。是真数据与假数据的线性混合。
论文:https://arxiv.org/pdf/1712.01026.pdf
代码:
发表:2018

在计算机视觉的许多领域中,生成对抗性网络已经取得了巨大的成功,其中WGANs系列被认为是最先进的,主要是由于其理论贡献和竞争的定性表现。然而,通过 Wasserstein-1 度量(W-met)来近似 k-Lipschitz约束是非常具有挑战性的。作者提出了一种新的 Wasserstein 散度(W-div),它是W-met的松弛版本,不需要k-Lipschitz约束。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。